Butterworth filter

The frequency response plot from Butterworth's 1930 paper.

The Butterworth filter is a type of signal processing filter designed to have a frequency response that is as flat as possible in the passband. It is also referred to as a maximally flat magnitude filter. It was first described in 1930 by the British engineer and physicist Stephen Butterworth in his paper entitled "On the Theory of Filter Amplifiers".

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618033988749...$(OEIS: A001622)

The $n$th Butterworth polynomial can also be written as a sum

$B_{n}(s)=\sum _{k=0}^{n}a_{k}s^{k}\,,$

with its coefficients $a_{k}$ given by the recursion formula

${\frac {a_{k+1}}{a_{k}}}={\frac {\cos(k\gamma )}{\sin((k+1)\gamma )}}$

and by the product formula

$a_{k}=\prod _{\mu =1}^{k}{\frac {\cos((\mu -1)\gamma )}{\sin(\mu \gamma )}}\,,$

where

$a_{0}=1\qquad {\text{and}}\qquad \gamma ={\frac {\pi }{2n}}\,.$

Further, $a_{k}=a_{n-k}$. The rounded coefficients $a_{k}$ for the first 10 Butterworth polynomials $B_{n}(s)$ are:

Butterworth Coefficients $a_{k}$ to Four Decimal Places

$n$	$a_{0}$	$a_{1}$	$a_{2}$	$a_{3}$	$a_{4}$	$a_{5}$	$a_{6}$	$a_{7}$	$a_{8}$	$a_{9}$	$a_{10}$
$1$	$1$	$1$
$2$	$1$	$1.4142$	$1$
$3$	$1$	$2$	$2$	$1$
$4$	$1$	$2.6131$	$3.4142$	$2.6131$	$1$
$5$	$1$	$3.2361$	$5.2361$	$5.2361$	$3.2361$	$1$
$6$	$1$	$3.8637$	$7.4641$	$9.1416$	$7.4641$	$3.8637$	$1$
$7$	$1$	$4.4940$	$10.0978$	$14.5918$	$14.5918$	$10.0978$	$4.4940$	$1$
$8$	$1$	$5.1258$	$13.1371$	$21.8462$	$25.6884$	$21.8462$	$13.1371$	$5.1258$	$1$
$9$	$1$	$5.7588$	$16.5817$	$31.1634$	$41.9864$	$41.9864$	$31.1634$	$16.5817$	$5.7588$	$1$
$10$	$1$	$6.3925$	$20.4317$	$42.8021$	$64.8824$	$74.2334$	$64.8824$	$42.8021$	$20.4317$	$6.3925$	$1$

The normalized Butterworth polynomials can be used to determine the transfer function for any low-pass filter cut-off frequency $\omega _{c}$, as follows

$H(s)={\frac {G_{0}}{B_{n}(a)}}$ , where $a={\frac {s}{\omega _{c}}}.$

Transformation to other bandforms are also possible, see prototype filter.

Maximal flatness

Assuming $\omega _{c}=1$ and $G_{0}=1$, the derivative of the gain with respect to frequency can be shown to be

${\frac {dG}{d\omega }}=-nG^{3}\omega ^{2n-1}$

which is monotonically decreasing for all $\omega$ since the gain $G$ is always positive. The gain function of the Butterworth filter therefore has no ripple. The series expansion of the gain is given by

$G(\omega )=1-{\frac {1}{2}}\omega ^{2n}+{\frac {3}{8}}\omega ^{4n}+\ldots$

In other words, all derivatives of the gain up to but not including the 2$n$-th derivative are zero at $\omega =0$, resulting in "maximal flatness". If the requirement to be monotonic is limited to the passband only and ripples are allowed in the stopband, then it is possible to design a filter of the same order, such as the inverse Chebyshev filter, that is flatter in the passband than the "maximally flat" Butterworth.

High-frequency roll-off

Again assuming $\omega _{c}=1$, the slope of the log of the gain for large $\omega$ is

$\lim _{\omega \rightarrow \infty }{\frac {d\log(G)}{d\log(\omega )}}=-n.$

In decibels, the high-frequency roll-off is therefore 20$n$ dB/decade, or 6$n$ dB/octave (the factor of 20 is used because the power is proportional to the square of the voltage gain; see 20 log rule.)

Minimum order

To design a Butterworth filter using the minimum required number of elements, the minimum order of the Butterworth filter may be calculated as follows.

$n=\left\lceil {\frac {\log {{\bigr (}{\frac {10^{\alpha _{s}/10}-1}{10^{\alpha _{p}/10}-1}}}{\bigr )}}{2\log {(\omega _{s}/\omega _{p})}}}\right\rceil$

where:

$\omega _{p}$ and $\alpha _{p}$ are the pass band frequency and attenuation at that frequency in dB.

$\omega _{s}$ and $\alpha _{s}$ are the stop band frequency and attenuation at that frequency in dB.

$n$ is the minimum number of poles, the order of the filter.

$\lceil \cdot \rceil$ denotes the ceiling function.

Nonstandard cutoff attenuation

The cutoff attenuation for Butterworth filters is usually defined to be −3.01 dB. If it is desired to use a different attenuation at the cutoff frequency, then the following factor may be applied to each pole, whereupon the poles will continue to lie on a circle, but the radius will no longer be unity. The cutoff attenuation equation may be derived through algebraic manipulation of the Butterworth defining equation stated at the top of the page.

$${\begin{aligned}p_{A}=p_{1}\times (10^{\alpha /10}-1)^{{-1}/{2n}}&\qquad {\text{For 0}}\leq \alpha <\infty \end{aligned}}$$

where:

$p_{A}$ is the relocated pole positioned to set the desired cutoff attenuation.

$p_{1}$ is a −3.01 dB cutoff pole that lies on the unit circle.

$\alpha$ is the desired attenuation at the cutoff frequency in dB (1 dB, 10 dB, etc.).

$n$ is the number of poles, the order of the filter.

Filter implementation and design

There are several different filter topologies available to implement a linear analogue filter. The most often used topology for a passive realisation is the Cauer topology, and the most often used topology for an active realisation is the Sallen–Key topology.

Cauer topology

Butterworth filter using Cauer topology

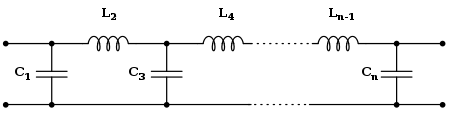
The Cauer topology uses passive components (shunt capacitors and series inductors) to implement a linear analog filter. The Butterworth filter having a given transfer function can be realised using a Cauer 1-form. The k-th element is given by

$C_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k={\text{odd}}$

$L_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k={\text{even}}.$

The filter may start with a series inductor if desired, in which case the L_k are k odd and the C_k are k even. These formulae may usefully be combined by making both L_k and C_k equal to g_k. That is, g_k is the immittance divided by s.

$g_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k=1,2,3,\ldots ,n.$

These formulae apply to a doubly terminated filter (that is, the source and load impedance are both equal to unity) with ω_c = 1. This prototype filter can be scaled for other values of impedance and frequency. For a singly terminated filter (that is, one driven by an ideal voltage or current source) the element values are given by

$g_{j}={\frac {a_{j}a_{j-1}}{c_{j-1}g_{j-1}}}\qquad j=2,3,\ldots ,n$

where

$g_{1}=a_{1}$

and

$a_{j}=\sin \left[{\frac {(2j-1)}{2n}}\pi \right]\qquad j=1,2,3,\ldots ,n$

$c_{j}=\cos ^{2}\left[{\frac {j}{2n}}\pi \right]\qquad j=1,2,3,\ldots ,n.$

Voltage driven filters must start with a series element and current driven filters must start with a shunt element. These forms are useful in the design of diplexers and multiplexers.

Sallen–Key topology

Sallen–Key topology

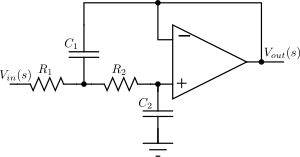
The Sallen–Key topology uses active and passive components (noninverting buffers, usually op amps, resistors, and capacitors) to implement a linear analog filter. Each Sallen–Key stage implements a conjugate pair of poles; the overall filter is implemented by cascading all stages in series. If there is a real pole (in the case where $n$ is odd), this must be implemented separately, usually as an RC circuit, and cascaded with the active stages.

For the second-order Sallen–Key circuit shown to the right the transfer function is given by

$H(s)={\frac {V_{\text{out}}(s)}{V_{\text{in}}(s)}}={\frac {1}{1+C_{2}(R_{1}+R_{2})s+C_{1}C_{2}R_{1}R_{2}s^{2}}}.$

We wish the denominator to be one of the quadratic terms in a Butterworth polynomial. Assuming that $\omega _{c}=1$, this will mean that

$C_{1}C_{2}R_{1}R_{2}=1\,$

and

$C_{2}(R_{1}+R_{2})=-2\cos \left({\frac {2k+n-1}{2n}}\pi \right).$

This leaves two undefined component values that may be chosen at will.

Butterworth lowpass filters with Sallen–Key topology of third and fourth order, using only one op amp, are described by Huelsman, and further single-amplifier Butterworth filters also of higher order are given by Jurišić et al.

Digital implementation

Digital implementations of Butterworth and other filters are often based on the bilinear transform method or the matched Z-transform method, two different methods to discretize an analog filter design. In the case of all-pole filters such as the Butterworth, the matched Z-transform method is equivalent to the impulse invariance method. For higher orders, digital filters are sensitive to quantization errors, so they are often calculated as cascaded biquad sections, plus one first-order or third-order section for odd orders.

Comparison with other linear filters

Properties of the Butterworth filter are:

• Monotonic amplitude response in both passband and stopband
• Quick roll-off around the cutoff frequency, which improves with increasing order
• Considerable overshoot and ringing in step response, which worsens with increasing order
• Slightly non-linear phase response
• Group delay largely frequency-dependent

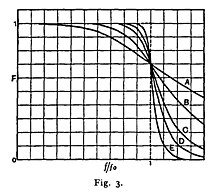
Here is an image showing the gain of a discrete-time Butterworth filter next to other common filter types. All of these filters are fifth-order.

The Butterworth filter rolls off more slowly around the cutoff frequency than the Chebyshev filter or the Elliptic filter, but without ripple.

See also

• Bessel filter
• Chebyshev filter
• Comb filter
• Elliptic filter
• Filter design